Определение моментов инерции относительно главных центральных осей швеллера

Определение моментов инерции является важной задачей в механике и используется при анализе динамики тел. Момент инерции характеризует способность тела сопротивляться изменению скорости вращения вокруг оси и зависит от распределения массы относительно этой оси. В данной статье рассмотрим способы определения моментов инерции швеллера, который является одним из наиболее популярных металлических профилей в строительстве.

Швеллер представляет собой прокатный профиль, имеющий в поперечном сечении форму буквы "Ш". Масса швеллера распределена неравномерно, что влияет на его моменты инерции относительно различных осей. Для определения моментов инерции швеллера необходимо знать его геометрические параметры, такие как ширина и высота полок, толщина стенок и размеры ребер жесткости.

Одним из простейших способов определения моментов инерции швеллера является использование теоремы Штейнера. Согласно этой теореме, момент инерции тела относительно определенной оси можно выразить через момент инерции относительно параллельной оси, проходящей через центр масс, и массу тела. Для швеллера необходимо определить моменты инерции относительно главных центральных осей, которые проходят через центр масс и перпендикулярны плоскости профиля.

Основные моменты инерции швеллера

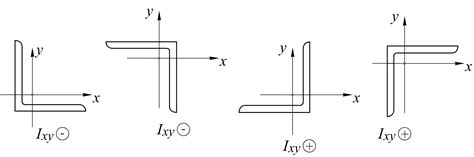
Момент инерции швеллера – это физическая величина, описывающая его сопротивление к вращательному движению относительно осей, проходящих через его центр масс. В зависимости от положения осей момент инерции может меняться и имеет основные направления: основные центральные оси.

Основными центральными осями в швеллере являются главные центральные оси, которые проходят через его центр масс. В зависимости от формы швеллера, оси могут быть разные и иметь разные направления.

Основные моменты инерции швеллера относительно главных центральных осей обозначаются как Iz, Iy и Ix. Из них Iz – момент инерции относительно оси, проходящей через центр масс и перпендикулярной плоскости швеллера. Iy – момент инерции относительно оси, проходящей через центр масс и параллельной главной плоскости швеллера. Ix – момент инерции относительно оси, проходящей через центр масс и перпендикулярной главной плоскости швеллера.

Знание основных моментов инерции швеллера позволяет определить его механические свойства и использовать в инженерных расчетах. Моменты инерции швеллера могут быть различными в зависимости от его размеров и конструктивных параметров.

Общая информация о швеллерах

Швеллер - это металлический профиль с двумя параллельными гранями и поперечным сечением в форме буквы "C". Швеллеры обладают высокой жесткостью и прочностью, что делает их идеальным материалом для использования в строительстве и машиностроении.

В основном, швеллеры используются в сварных конструкциях, где они играют роль балок, стоек или брусьев. Они хорошо подходят для создания мостов, рам зданий, каркасов и других конструкций, где требуется высокая прочность и устойчивость к нагрузкам.

Швеллеры выпускаются из различных материалов, включая сталь, алюминий и нержавеющую сталь. Каждый из этих материалов обладает своими уникальными свойствами, что делает их подходящими для разных задач.

Для определения моментов инерции швеллера относительно главных центральных осей необходимо знать размеры и геометрические параметры профиля. Это позволяет рассчитать моменты инерции, которые являются важными характеристиками при расчете прочности и жесткости конструкций.

Общая информация о швеллерах позволяет понять их применение и использование в различных областях строительства и машиностроения. Каждый вид швеллера имеет свои особенности и характеристики, которые необходимо учесть при проектировании и изготовлении конструкций.

Что такое момент инерции?

Момент инерции – это фундаментальная физическая величина, характеризующая способность тела сопротивляться изменению своего вращательного состояния относительно оси. Он определяет инертность тела по отношению к вращательному движению и зависит от его формы и распределения массы. Момент инерции можно рассматривать как аналог массы для вращательного движения.

Момент инерции обычно обозначается символом I и измеряется в кг∙м². Он зависит от геометрических параметров тела и его массы. Чем больше масса распределена относительно оси вращения, тем выше момент инерции. Например, удлинение тела увеличивает его момент инерции, так как масса становится более удаленной от оси вращения.

Момент инерции является важным понятием в механике и находит применение в различных областях науки и техники. Он используется для расчета вращательных движений твёрдых тел, прогнозирования и управления движениями механических систем, проектирования механизмов и машин.

Момент инерции может быть определен для различных форм тел, включая простые геометрические фигуры, такие как круги, прямоугольники, цилиндры, а также сложные формы, например, швеллеры. Он может быть вычислен аналитически с использованием специальных формул или экспериментально с помощью физических измерений.

Способы определения момента инерции

Момент инерции — это физическая величина, характеризующая инерцию вращательного движения тела относительно его оси вращения. Для определения момента инерции швеллера относительно главных центральных осей существуют несколько методов.

Один из способов определения момента инерции швеллера - это использование геометрических характеристик фигур, составляющих его сечение. При этом все составляющие элементы сечения швеллера рассматриваются как точечные массы, расположенные на разных расстояниях от оси вращения. С помощью формулы, учитывающей расстояние от оси вращения до каждого элемента, можно определить момент инерции швеллера относительно главных центральных осей.

Еще одним способом определения момента инерции швеллера является использование теоремы Штейнера. Эта теорема позволяет найти момент инерции относительно нужной оси, зная момент инерции относительно параллельной оси и расстояние между этими осями. Для швеллера можно использовать эту теорему, если известен момент инерции относительно оси, проходящей через его центр масс, а также дистанция между этой осью и нужной осью вращения.

Также существуют таблицы, в которых приведены значения моментов инерции для различных геометрических фигур. Если швеллер можно представить как комбинацию таких фигур, можно воспользоваться этими таблицами для определения момента инерции. Необходимо выразить момент инерции швеллера как сумму моментов инерции отдельных фигур с учетом их геометрических параметров и расположения относительно оси вращения. Такой метод позволяет более точно и быстро определить момент инерции.

Основные центральные оси швеллера

Центральные оси швеллера - это оси, относительно которых определяется момент инерции данного сечения. Для швеллера существуют три главных центральных оси, которые называются главными моментными оси.

Первая главная моментная ось – это главная ось симметрии швеллера, проходящая через его центр масс. Такая ось является одной из осей симметрии, параллельных плоскости изгиба и проходящих через сам центр швеллера.

Вторая и третья главные моментные оси – это главные оси инерции, проходящие через центры тяжести параллельных полос. Плоскость каждой из таких осей проходит через центральную плоскость швеллера и перпендикулярна ей. Они лежат в сагиттальной плоскости и расположены симметрично относительно горизонтальной оси симметрии.

Зная координаты центра масс и значение моментов инерции относительно каждой из главных моментных осей, можно рассчитать моменты инерции относительно любых других осей с использованием формул преобразования моментов инерции.

Главные центральные оси момента инерции

Главные центральные оси момента инерции – это оси, относительно которых момент инерции тела имеет наименьшее значение. Они являются основными осями симметрии и позволяют описать поведение тела при его вращении в пространстве.

Главные центральные оси момента инерции связаны с тремя основными направлениями пространства: осью X, осью Y и осью Z. Ось X соответствует наименьшему моменту инерции, ось Z – наибольшему, а ось Y – промежуточному значению.

Информация о главных центральных осях момента инерции является важной для различных инженерных расчетов и конструкций. Например, при проектировании механизмов, вращающихся вокруг различных осей, необходимо знать главные центральные оси момента инерции для определения момента сопротивления.

Для некоторых геометрических фигур, таких как швеллер, главные центральные оси момента инерции могут быть представлены в виде таблицы. Такая таблица содержит значения моментов инерции относительно каждой оси, а также информацию о координатах центра масс.

В результате, зная главные центральные оси момента инерции швеллера, можно провести анализ его поведения при вращении в пространстве и принять соответствующие меры для обеспечения его устойчивости и надежности при эксплуатации.

Формулы для определения момента инерции швеллера

Момент инерции швеллера является важным параметром при проектировании и расчете различных конструкций. Он характеризует способность швеллера сопротивляться искривлению под действием внешних нагрузок. Формулы для определения момента инерции швеллера позволяют рассчитать этот параметр с высокой точностью.

Момент инерции швеллера относительно осей X и Y можно вычислить с помощью следующих формул:

1. Момент инерции швеллера относительно оси X (Ix) рассчитывается по формуле:

Ix = Ixx + A * h^2

где Ixx - момент инерции прямоугольной части швеллера относительно оси X;

A - площадь поперечного сечения швеллера;

h - высота поперечного сечения швеллера.

2. Момент инерции швеллера относительно оси Y (Iy) вычисляется по формуле:

Iy = Iyy + A * b^2

где Iyy - момент инерции прямоугольной части швеллера относительно оси Y;

b - ширина поперечного сечения швеллера.

В случае, когда швеллер имеет дополнительные отверстия или вырезы, формулы для определения момента инерции немного сложнее и требуют учета дополнительных параметров. Кроме того, для швеллеров с переменной высотой или шириной поперечного сечения необходимо применять специальные формулы.

Вычисление момента инерции швеллера по указанным формулам позволяет учесть его геометрические особенности и получить более точные результаты при проектировании и расчете конструкций, использующих швеллеры.

Примеры расчетов момента инерции для разных осей

Пример 1. Рассмотрим швеллер с геометрическими параметрами: высотой (h) – 200 мм, шириной полки (b) – 100 мм, толщиной полки (t) – 10 мм, и толщиной стенки (tw) – 5 мм. Предположим, что мы хотим найти момент инерции относительно главной центральной оси, проходящей через центр масс швеллера.

В данном примере можно воспользоваться формулой для момента инерции относительно оси, параллельной и проходящей через центр масс. Будем обозначать момент инерции относительно данной оси как I_cm. По формуле:

I_cm = (b * h³ - (b - tw) * (h - 2 * tw)³) / 12

Подставляя числовые значения:

• h = 200 мм (0.2 м)
• b = 100 мм (0.1 м)
• t = 10 мм (0.01 м)
• tw = 5 мм (0.005 м)

Можно получить конечное значение момента инерции I_cm в кг•м².

Пример 2. Рассмотрим швеллер с другими геометрическими параметрами: высотой (h) – 150 мм, шириной полки (b) – 80 мм, толщиной полки (t) – 12 мм, и толщиной стенки (tw) – 8 мм. Снова предположим, что нам необходимо найти момент инерции относительно главной центральной оси, проходящей через центр масс швеллера.

В данном случае можно использовать ту же формулу, но подставлять новые значения параметров:

• h = 150 мм (0.15 м)
• b = 80 мм (0.08 м)
• t = 12 мм (0.012 м)
• tw = 8 мм (0.008 м)

Расчетный результат даст нам момент инерции I_cm для данного швеллера.

И таким образом, путем подстановки различных значений геометрических параметров, можно рассчитать момент инерции для разных осей.

Выводы и рекомендации по использованию момента инерции швеллера

Момент инерции швеллера является важным параметром при расчете его прочностных характеристик. Момент инерции позволяет определить способность швеллера сопротивлять изгибающим нагрузкам и сохранять свою форму при воздействии сил.

При использовании момента инерции швеллера следует учитывать его значимость для расчета прочности и деформаций конструкций. Чем больше момент инерции швеллера, тем более жестким и прочным будет каркас в целом.

Рекомендуется выбирать швеллер с большим моментом инерции для строительных конструкций, которые подвержены значительным нагрузкам. В таких случаях использование швеллеров с большим моментом инерции позволит снизить деформации и увеличить прочность конструкции.

Момент инерции швеллера также влияет на стоимость конструкции. Швеллеры с большим моментом инерции обычно стоят дороже, но это дополнительные затраты оправдываются повышенной прочностью и долговечностью конструкции.

Таким образом, при выборе швеллера следует обратить внимание на его момент инерции и адаптировать его к требованиям и условиям конкретного проекта. Не стоит экономить на прочности конструкции, ведь это может повлечь за собой серьезные последствия и увеличенные затраты на ремонт и замену поврежденных элементов.

Вопрос-ответ

Как определить момент инерции швеллера относительно главных центральных осей?

Момент инерции швеллера относительно главных центральных осей можно определить с помощью соответствующих формул и уравнений, исходя из геометрических параметров швеллера. Для этого нужно знать размеры швеллера и использовать математические выражения, связанные с моментом инерции и массой тела.

Какие данные нужны для определения момента инерции швеллера относительно главных центральных осей?

Для определения момента инерции швеллера относительно главных центральных осей необходимо знать следующие данные: массу швеллера, его геометрические параметры, такие как длина, ширина и высота, а также расстояние от осей вращения до различных точек швеллера. Также может понадобиться информация о распределении массы внутри швеллера.

Какие формулы используются для расчета момента инерции швеллера относительно главных центральных осей?

Для расчета момента инерции швеллера относительно главных центральных осей могут использоваться различные формулы в зависимости от формы и размеров швеллера. Например, для прямоугольного швеллера можно использовать формулу I = (1/12) * m * (b^2 + h^2), где I - момент инерции, m - масса швеллера, b - ширина швеллера, h - высота швеллера.

Что представляет собой момент инерции швеллера относительно главных центральных осей?

Момент инерции швеллера относительно главных центральных осей представляет собой физическую величину, которая характеризует распределение массы вокруг осей вращения. Он позволяет определить, насколько трудно изменить состояние движения швеллера относительно данных осей. Чем больше момент инерции, тем большие усилия необходимы для изменения движения швеллера.

Зависит ли момент инерции швеллера относительно главных центральных осей от его массы?

Да, момент инерции швеллера относительно главных центральных осей зависит от его массы. Чем больше масса швеллера, тем больше момент инерции, так как большая масса означает большее сопротивление изменению движения. Однако масса не является единственным фактором, влияющим на момент инерции - геометрические параметры швеллера также играют важную роль в его определении.