Прогиб листового металла – один из наиболее распространенных процессов в металлообработке. Этот метод позволяет придавать заготовкам нужную форму и размер, что делает его незаменимым на производстве. В процессе прогиба необходимо правильно рассчитать параметры заготовки, чтобы избежать деформаций и прочих нежелательных эффектов.
Основные методы расчета листового металла на прогиб включают использование формул, таблиц и специализированных программных инструментов. В первую очередь, необходимо определить материал, из которого изготовлена заготовка, его толщину и механические свойства. Затем следует выбрать подходящий метод прогиба: воздушным прессом, гидравлическим прессом или другими способами.
При расчете прогиба листового металла учитываются такие параметры, как радиус гиба, угол гиба, длина заготовки и коэффициент упругости материала. Применение правильных формул и учет всех необходимых факторов позволяет получить точные результаты и избежать непредвиденных ситуаций на производстве.
Важно отметить, что расчет листового металла на прогиб – сложный и ответственный процесс, требующий опыта и профессионализма. В случае сомнений или недостатка знаний лучше обратиться за консультацией к специалистам, которые смогут помочь в определении всех нужных параметров и выборе оптимального метода прогиба.
Методы расчета листового металла на прогиб
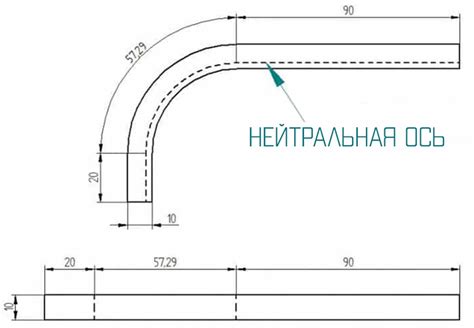
При проектировании и изготовлении различных конструкций из листового металла часто возникает необходимость расчета прогиба. Это важная задача, так как правильный расчет гарантирует прочность и устойчивость конструкции.
Существует несколько основных методов расчета листового металла на прогиб, которые используются в инженерии и металлообработке.
- Аналитический метод. Этот метод основан на использовании математических формул для расчета прогиба. Для каждой конкретной ситуации задаются геометрические параметры листа, его материал, а также условия нагрузки. На основе этих данных проводится анализ напряжений и деформаций и получается значение прогиба.
- Экспериментальный метод. Этот метод основан на проведении физических экспериментов с листовым материалом. С помощью специального оборудования измеряются деформации и напряжения при различных нагрузках. Полученные данные позволяют определить коэффициенты, которые затем используются для расчета прогиба.
- Метод конечных элементов. Этот метод основан на разбиении листа на множество маленьких элементов, для каждого из которых решаются уравнения механики деформируемого тела. Затем полученные значения объединяются и используются для определения прогиба листа в целом. Этот метод позволяет учитывать сложные геометрические формы и неоднородности материала.
При выборе метода расчета листового металла на прогиб необходимо учитывать конкретные условия и требования к конструкции. В каждом случае может быть оптимальным использование одного или нескольких методов совместно.
Основные формулы и принципы работы
Расчет листового металла на прогиб является важной задачей при проектировании и изготовлении металлических конструкций. Для успешного выполнения расчета необходимо учесть несколько основных формул и принципов работы.
- Модуль упругости материала: расчет прогиба листового металла в значительной степени зависит от его модуля упругости. Чем выше модуль упругости, тем меньше будет прогиб при одинаковой нагрузке.
- Геометрические параметры листового металла: для расчета прогиба необходимо знать толщину, ширину и длину листа металла. Эти параметры влияют на его жесткость, что в свою очередь влияет на прогиб.
- Распределение нагрузки: равномерное распределение нагрузки на листовой металл приводит к однородному прогибу, тогда как неравномерное распределение может привести к нежелательным деформациям.
- Методы расчета: существует несколько методов расчета прогиба листового металла, включая метод пластической теории прогиба, метод теории упругости и метод конечных элементов. Каждый из них имеет свои преимущества и ограничения, и выбор метода зависит от конкретной ситуации.
Важно отметить, что расчет прогиба листового металла является сложным процессом, который требует знания физических и математических основ, а также опыта в применении соответствующих формул. Правильный расчет обеспечивает безопасность и надежность металлических конструкций, а также помогает избежать деформаций и повреждений. При необходимости рекомендуется обратиться к специалисту для получения квалифицированной помощи в процессе расчета.
Вопрос-ответ
Как правильно рассчитать прогиб листового металла?
Для расчета прогиба листового металла можно использовать различные методы. Один из основных методов - это метод прямоугольников. Для этого следует измерить основные параметры листа, такие как толщина, ширина и длина, а также учитывать материал и его удельное сопротивление. После этого применяют специальные формулы, чтобы рассчитать необходимый прогиб и выбрать соответствующий пресс или станок для изготовления изделия.
Какие формулы используются для расчета прогиба листового металла?
Для расчета прогиба листового металла используются различные формулы, в зависимости от выбранного метода. Например, для метода прямоугольников применяется следующая формула: W = (k * L^2) / (8 * h), где W - величина прогиба, k - коэффициент, зависящий от материала, L - длина листа, h - толщина листа. Другие методы могут использовать другие формулы для расчета прогиба.
Как выбрать подходящий пресс для изготовления изделия из листового металла?
Для выбора подходящего пресса для изготовления изделия из листового металла нужно учитывать несколько параметров. В первую очередь следует определить требуемую силу прогиба, которая зависит от толщины и материала листа, а также от его размеров. Также важно учесть тип пресса и его возможности в работе с определенными материалами и размерами листа. В процессе выбора пресса можно обратиться к специалистам или изучить технические характеристики различных моделей прессов.
Какие преимущества и недостатки имеют различные методы расчета прогиба листового металла?
У различных методов расчета прогиба листового металла есть свои преимущества и недостатки. Например, метод прямоугольников довольно прост в применении и требует минимальных затрат на оборудование. Однако он может быть неточным для сложных форм и особых материалов. В то же время, метод конечных элементов может быть более точным, но требует сложных вычислений и специального программного обеспечения.